Goodbye C developers: The future of programming with certified program synthesis
#projects #research #coq #verificationIntroduction
Another day, another dime, another Major. Security. Vulnerability. All caused by stubborn C developers refusing to abandon their outdated programming language.

But wait! I hear you cry, the C-programming language forms an integral part of the foundations of our ecosystem; countless billions of lines of C code underlie much of the technology that upholds our modern society.
Who else but these masters of code, these witches and wizards of the wire, these lords of low-level coding could we trust to write this code?
Note: To be clear, this post isn't in advocacy of a copy-and-paste statistical approach to code generation with no guarantees of correctness (like the recently released Copilot), but rather a semantic-aware certified synthesis that produces correct code 100% of the time
Let's write some C code!
How hard can writing C code actually be?
Well, why don't we have a look.
Let's consider the following snippet — a simple, standard, procedure to copy a linked list:
void listcopy(void **r) { void *x2 = *r; if (x2 == NULL) { return; } else { int vx22 = *(int *)x2; void *nxtx22 = *((void **)x2+1); *r = nxtx22; listcopy(r); void *y12 = *(void **)r; void *y2 = (void *) malloc(2 * sizeof(void *)); *r = y2; *((int *)y2) = vx22; *((void **)y2+1) = y12; return; } }
Surely, that's not too hard to understand? After all, it's just a bit of pointer twiddling, a malloc or two, and a single recursive call - what could be more simple?
Do you understand how this code works?
Are you sure?
Would you have been able to tell if I removed one of the statements? (or have I already removed a statement and just not told you?).
The point I'm trying to make here is that pointer-manipulating code can often be complex and convoluted, even for simple operations such as copying a linked list. These kinds of complexities provide ample opportunity for bugs to sneak in, and can make it difficult to trust code written by C-developers.
Certified Program Synthesis to the rescue!
As it turns out, this is in fact possible! In our latest research - "Certifying the synthesis of heap-manipulating programs" by Yasunari Watanabe, myself, George Pîrlea, Nadia Polikarpova, and Ilya Sergey, we tentatively answer this question in the affirmative, developing a novel tool (available here) for automatically synthesising completely correct C-code in a mere matter of seconds. Additionally, to provide trust in the generated code, inspired by early work on proof-carrying-code, the tool also outputs independently verifiable proof-certificates for each synthesised program, which then formally guarantee that the generated code must satisfy its functional specifications. These certificates are written in Coq, a well-established formal proof assistant that has been used for several significant developments in mathematics and software engineering (CompCert, CertiKOS etc.), and serves as one of the de-facto means that humanity has to ensure absolute correctness of code.

In fact, the code written above was actually entirely automatically synthesised by our tool, along with a proof certificate, formally guaranteeing its correctness. As end users of the tool, we didn't even have to bother reasoning about how exactly it did its pointer manipulations, and instead could rely on the formal certificate to guarantee that it would indeed correctly copy a linked list.
In other words, given a specification to copy a list, our synthesis tool was able to produce a complete self-contained C program with a separate independent proof certificate, formally guaranteeing, without a shadow of a doubt, that it fully satisfies the specification, thereby removing any need to trust a fallible human developer.
This is the future of coding!
The rest of this post…
So how on earth does this work? Is it Machine Learning? GPT3? Some advanced form of GOFAI?
As it turns out, this actually all just boils down to a rather clever composition of various aspects of Programming Languages theory - in particular, separation logic, deductive synthesis and constructive proofs.
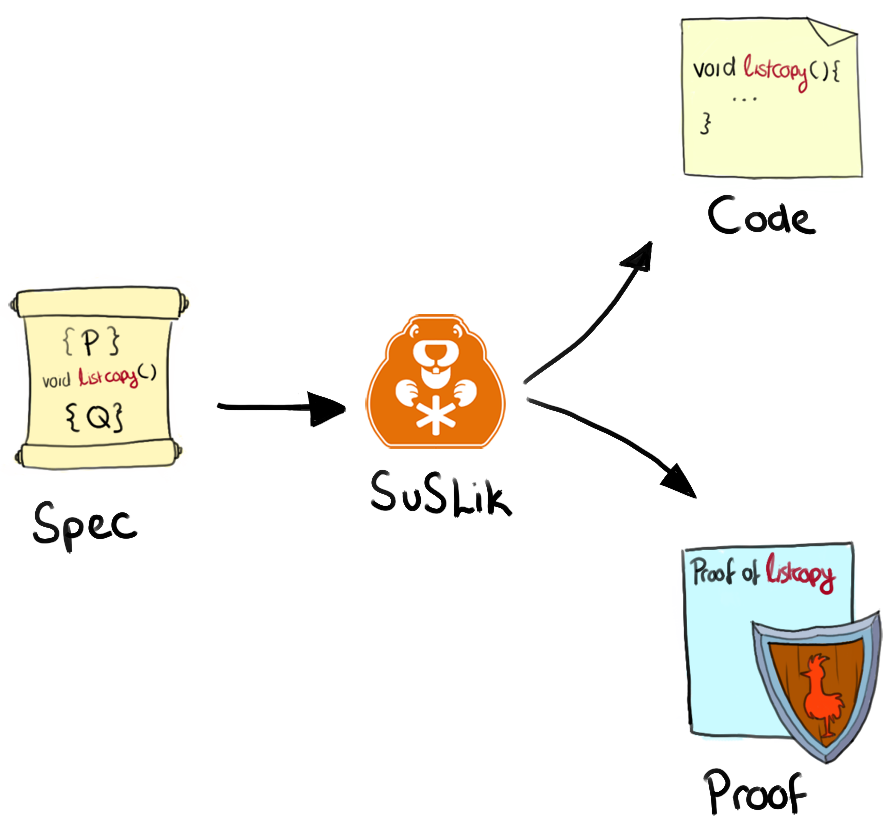
In the rest of this post, we'll provide a high-level overview of this work, starting with an introduction to theory on which this research builds, the general technique used to construct certified C programs and finally discussing the limitations and potential directions in which this work could be extended.
Warning: What you are about to read is bleeding-edge research. The following is a sneak peak of what the future will look like, but it may be a while before it will reach end users.
Reasoning about pointers: An introduction to separation logic
Our journey begins with a simple problem: How can we reason about memory and pointers in a formal fashion?
When programmers write code, they intuitively have some kind of mental model of memory and pointers in their mind that they use to reason about programs – thus in order to synthesise and certify these kinds of heap-manipulating programs, we'll first need to work out how to encode this mental model within a formal logic.
The solution that PL research has converged upon is this notion known as *separation logic*, a particular type of formal logic specialised to capture the ways in which developers reason about pointers, and in the rest of this section, we'll provide a whistle stop tour of the fundamental concepts of this logic as it relates to this work.
Points to & Memory blocks
Naturally, given our desire to reason about heap-manipulating programs, the core building block of separation logic is this notion of a points-to relation.
We write x :-> y, read as "x points to y", to
denote the fact that the memory address x maps to a memory cell
containing the value y.

Different variations of separation logic have different choices of specific notation — here, for simplicity, we'll introduce some additional notation to allow explicitly referencing contiguous blocks of memory.
We write [x; n] to denote the fact that the the
memory address x maps to the start of a block of n contiguous cells in
memory.
We can then specify the individual values of each of these cells by
adding an offset index - i.e. (x + i) :-> a.
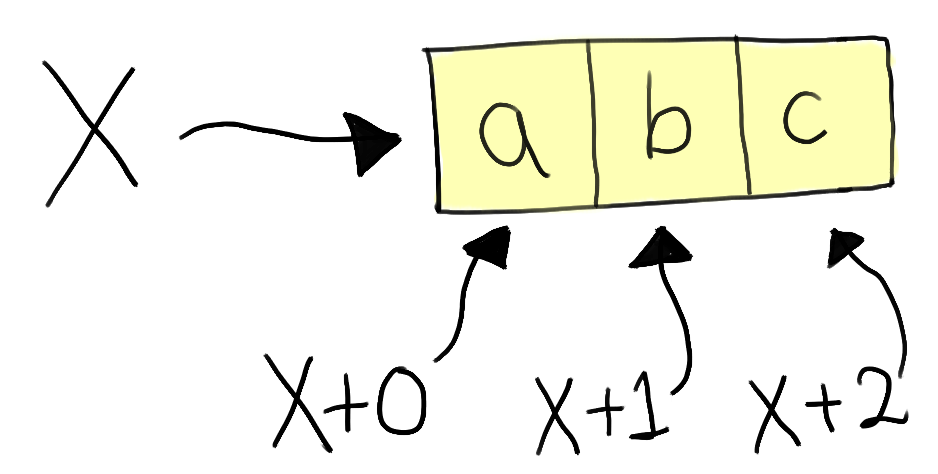
These are typically referred to as spatial assertions or heap assertions, as they each assert some kind of property on the heap.
Separating Conjunct
All that I've presented so far probably seems pretty straightforward, however there's one additional component that we're still missing - in particular, a mechanism for composing spatial assertions together, and this is exactly where the true novelty of separation logic lies.
When we start trying to compose spatial assertions together, we start to have to reason about how these assertions may influence each other, and this can cause problems.

So far, we've assumed that each spatial assertion, i.e. x :-> y, asserts that some particular property holds over the
heap, in this case that the memory address x
contains the value y.
The problem with this reasoning is that if each spatial assertion holds over the entire heap, then checking the validity of a arbitrary collection of spatial assertions can become very hairy, as it requires one to reason about all the assertions at once and determine if they hold over the entire heap. In particular, the issue is that this model lacks compositionality.
To fix this problem, separation logic instead proposes that spatial assertions apply over subsets of the entire heap, and introduces a special construct, the separating conjunct, to allow denotating that assertions hold over disjoint subsets of the heap.
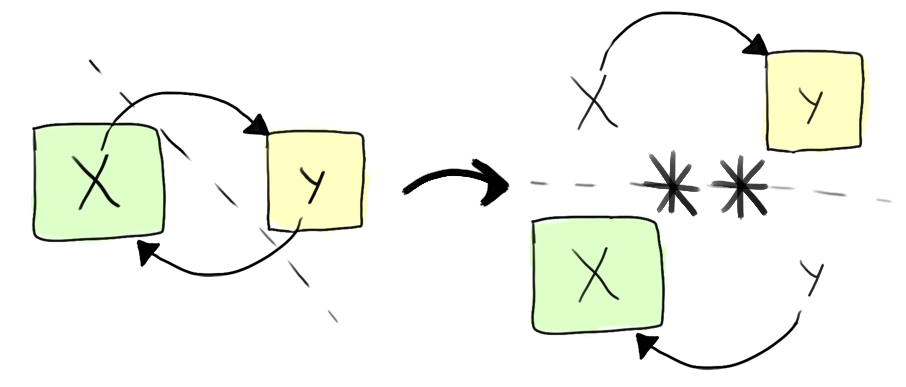
The separating conjunct, written P ** Q, is
conceptually fairly simple. All it asserts is that there exists some
partitioning of the entire heap, such that one can make spatial
assertions P and Q both
true. This then restores compositionality of analysis, as we can
reason about individual assertions independently, as they must, by
definition, apply to disjoint subsets of the heap.
Spatial predicates
The final relevant part of separation logic for this work is a notion of spatial predicates which build on top of the basic foundations we've covered so far to allow logicians to encode more complex heap-based data structures.
As an example, consider the implementation of a spatial predicate
linked_list for encoding linked lists:
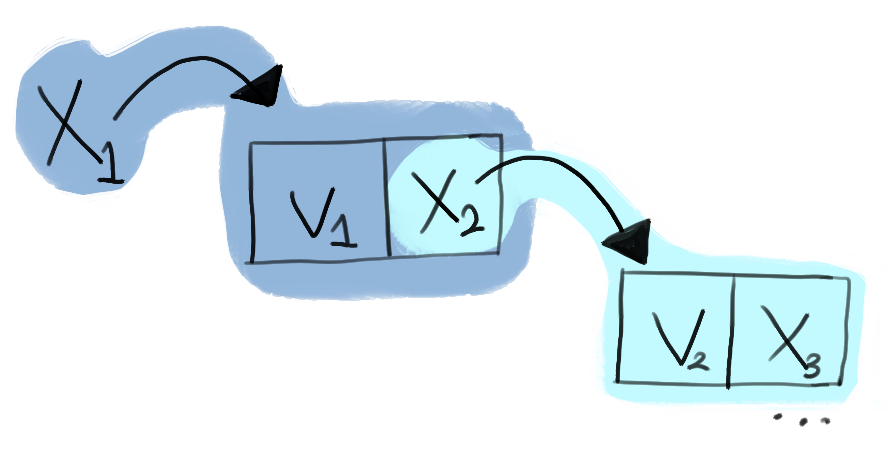
linked_list(x,S) =
| x == NULL -> emp; S = {}
| x != NULL ->
[x;2] ** x :-> v ** (x + 1) :-> y
** linked_list(y, S'); S = {v} ++ S'
Our predicate linked_list(x,S) asserts that the
memory address x denotes the start of a
linked-list with contents denoted by the set S.
To do this, it considers two separate cases:
- Case 1:
x == NULL, the base case, the empty list, which contains no elements, so setSmust be empty. - Case 2:
x != NULL, the inductive case, wherexis notNULL, and so:xmaps to a 2-element block of memory, where the first element is some valuevfrom the set, and the second element contains a memory locationyyitself is the head of another linked listlinked_list(y, S')which contains the remaining elements of the listS'.
As we can see, this simple spatial predicate is thereby able to capture any and all possible linked lists that could be constructed, by simply choosing the correct parameters and cases for each element of the list:
Putting all these components together, we now have a fairly expressive logic, which we can use to completely specify the behaviours of many standard C programs.
Putting it all together…
Now we have a better understanding of separation logic, we can try and formulate some kind of specification for list copy, to construct the synthesis task from the introduction.
// r :-> x ** linked_list(x,S) void listcopy(void **r) // r :-> y ** linked_list(y,S) ** linked_list(x,S)
In the above specification the comment before the function declaration specifies the pre-condition, the spatial assertions that are required to be true in order to call the operation, and the comment after represents the post-condition, the spatial assertion guaranteed to hold after executing the method.
Using the notations and definitions we covered earlier, we can now decipher each of these annotations fairly easily back into natural language:
- Precondition
- asserts that the argument
rmust map to a cell containing a memory locationx, and that location must denote the start of a linked listlinked_list(x,S). - Postcondition
- then asserts that after execution,
rshould now map to a cell containing a memory locationy, and that location must denote the start of a new linked listlinked_list(y,S), with the original linked listlinked_list(x,S)still present on the heap.
In summary, listcopy, given a pointer to a
linked list, must ensure that after executing the heap must contain
two copies of the original list — i.e. listcopy must copy a list.
Building programs with deductive reasoning: Suslik
As we have seen in the previous section, separation logic provides an excellent formalism for precisely specifying the semantics of C functions. This fact is widely exploited by the community, with separation logic forming the theoretical foundations of many verification frameworks. But verification of existing code is one thing, is it also possible to use the formalisms of separation logic for generating entirely new code?

As it turns out, the compositionality and modularity of separation logic means that it can actually be quite easily adapted to fit into a deductive-reasoning-based automated synthesis strategy. This insight was first identified by Nadia Polikarpova and Ilya Sergey, who then used it to develop SuSLik, a synthesis tool for generating heap-manipulating programs in a small toy language SuSLang. SuSLik forms the foundations on which we extend for this latest work, and so in the rest of this section, we will provide an overview of how its deductive-based synthesis works.
Deductive reasoning with Separation Logic
The core idea with deductive synthesis is to use specifications in separation logic to act as a guide during the synthesis process. This approach turns out to be quite efficient, because often the specifications found during synthesis can uniquely determine the program statements that are required to satisfy them.
As an example, let's work through the example of synthesising a swap function:
// x :-> a ** y :-> b void swap(int *x, int *y) { ??? } // x :-> b ** y :-> a
The goal for the synthesizer during the synthesis is to iteratively emit program statements that gradually change the pre and post-conditions, until they are eventually equal, at which point the synthesis is complete.
At the start, as the variables a and
b are not accessible by the program (as they are
stored within the cells denoted by both pointers), the only operation
that the synthesis procedure can do is to emit read operations to load
their values:
void swap(int *x, int *y) { int a = *x; int b = *y; // x :-> a ** y :-> b ??? } // x :-> b ** y :-> a
Now that a and b are
accessible, the synthesizer can try to unify individual spatial
assertions in the pre and post-conditions by using their values.
For example, we can unify the assertions x :-> a
in the pre-condition and x :-> b in the
post-condition by simply emitting a write to x:
void swap(int *x, int *y) { int a = *x; int b = *y; *x = b; // x :-> b ** y :-> b ??? } // x :-> b ** y :-> a
From here, if we repeat the same analysis for y :-> a, the synthesizer emits a write to y, and
we are left with:
void swap(int *x, int *y) { int a = *x; int b = *y; *x = b; *y = a; // x :-> b ** y :-> a ??? } // x :-> b ** y :-> a
At this point, the pre and post-condition are now equal, and so the synthesis is complete, leaving us with a complete standalone program:
void swap(int *x, int *y) { int a = *x; int b = *y; *x = b; *y = a; return; }
Synthesising list copy
It just so happens that this same reasoning procedure presented above for synthesising swap actually scales quite well, and can be directly used to verify more complex programs like list copy.
To illustrate how well this works let's have a look at the process of synthesising the base case of list copy from before:
// r :-> x ** linked_list(x,S) void listcopy(void **r) { ??? } // r :-> y ** linked_list(y,S) ** linked_list(x,S)
Following the same reasoning as before, the synthesis starts by emitting a read operation:
void listcopy(void **r) { void *x2 = *r; // r :-> x2 ** linked_list(x2,S) ??? } // r :-> y ** linked_list(y,S) ** linked_list(x2,S)
In order to proceed further, the synthesis must unfold the definition of the heap predicate for linked lists, and this naturally translates into an if-else-statement for each case of the predicate:
void listcopy(void **r) { void *x2 = *r; if (x2 == NULL) { // r :-> x2 ** emp; x2 == NULL && S = {} ??? // r :-> y ** linked_list(y,S) ** linked_list(x2,S) } ... }
For the base-case, the synthesis procedure can propagate the
equalities, x2 == NULL and S = {}, that the constructor exposes across both the pre and
post-condition without having to emit any new statements:
void listcopy(void **r) { void *x2 = *r; if (x2 == NULL) { // r :-> NULL ** emp ??? // r :-> y ** linked_list(y,{}) ** linked_list(NULL,{}) } ... }
At this point, the synthesis procedure notices that the linked_list(y,{}) predicate can be satisfied by instantiating
y with NULL:
void listcopy(void **r) { void *x2 = *r; if (x2 == NULL) { // r :-> NULL ** emp ??? // r :-> NULL ** emp } ... }
At this point, the pre and post-conditions are equal, and so the synthesis procedure knows that it has successfully synthesised the base case of the function:
// r :-> x ** linked_list(x,S) void listcopy(void **r) { void *x2 = *r; if (x2 == NULL) { return; } ... } // r :-> y ** linked_list(y,S) ** linked_list(x,S)
A similar search procedure can be done on the inductive case as well, and eventually leads to the original code presented in the introduction. The SuSLik paper also demonstrates this technique can be used to synthesise a variety of other complex algorithms, such as tree flattening, sorting, binary search trees etc.
Ensuring trust with synthesis certificates
So far we've seen how SuSLik can synthesise heap manipulating SuSLang programs – if we adjust the pretty printing, it wouldn't be too hard to produce C programs directly from SuSLik's synthesis output – but the real question is how can we trust these programs as being correct?
If we actually want to use SuSLik's output in real world programs, we need some kind of way of verifying that the synthesised programs are indeed correct – in other words, we need certified synthesis!
Approaches to certifying synthesis
Broadly speaking, there are two possible approaches one could take to certified synthesis – either that of certifying the synthesizer, or producing proof certificates.
- Certified Synthesizer
- The core idea with this approach is to encode the source code of the synthesizer itself with an formal setting and then prove additional properties about the validity of its synthesis procedure, such as ensuring that the programs it outputs will always satisfy the specifications that they are generated from.
- Proof Certificates
- An alternative approach to certified synthesis, first developed by early research work on proof-carrying code, is extend the synthesis procedure to also produce proofs of correctness for the synthesised programs. This way, users of the synthesised program can verify its correctness without having to trust the synthesizer by simply verifying the associated proof.
For our work, certifying the synthesis procedure was certainly a wildly impractical approach to the problem. The SuSLik project, while being relatively young, is a fairly mature software project, with the main branch having over 1000 commits, and it's source code collectively comprising over 10,000 lines of complex Scala code. Needless to say, even just the process of encoding SuSLik in a format amenable to verification would likely be an insurmountable task. Luckily, as it turns out, as the SuSLik synthesis procedure is based around deductive reasoning, it is far more tractable to extend SuSLik to produce proof certificates for its synthesised programs.
Aside: What's in a proof? or What does it mean to be correct, even?
So we've come to the conclusion that the only tractable way forward is to generate proof-certificates - additional, independently verifiable, build artefacts that can guarantee that a synthesised program is indeed correct – but what exactly does this mean? how can we even hope to guarantee the correctness of a given program?
As it turns out, this exact question — that of program verification – has been a /longstanding topic/ in Programming languages research, and much prior work has been done into various approaches to certifying the behaviour of programs, such as model-checking, formal verification, static analysis etc.
For this work, we focus on one particular type of verification strategy, proving the correctness of programs within the Coq proof assistant. Coq is a well-established tool that provides a formal language for writing machine-checked mathematical proofs and has been previously used for several significant developments in both mathematics (being used to prove the 4-colour theorem), and in software engineering (being used to implement a fully certified C compiler or constructing a certified OS etc.). When using it for verification, we encode the semantics of the target programming language within Coq's logic, and then use a proof script (a series of commands to the Coq kernel) to use the proof assistant to prove that the code satisfies the specification.
Obviously, as is the nature of reality, it is never possible to know with 100% certainty whether a given piece of code is entirely correct (as there could be bugs in the proof assistant itself), but in practice, certified programs written in Coq have consistently been empirically found to be completely free of the bugs that typically pervade other similarly sized projects. In other words… you can trust a Coq proof-certificate to guarantee the behaviour of the certified code.
Generating Proof Certificates
How can we leverage SuSLik's synthesis procedure to produce proof certificates?
Well the key idea here is that as SuSLik bases its synthesis procedure around the formalisms and logical rules of separation logic, the implicit reasoning that it performs during its search process is actually inherently quite close to the steps that a human might take while proving the correctness of a program in a separation logic-based verification framework.
Using this observation, we can then come up with a generic methodology for extending SuSLik to produce proof certificates for different verification backends: for each kind of synthesis rule that SuSLik uses during its search process to generate code, we can then map it to a corresponding proof rule that implements the corresponding operation in terms of the verification backend. Using this perspective, the entire certification process can be uniformly implemented in terms of a kind of specialised traversal over the synthesis tree, where a so-called "proof-interpreter" steps over each synthesis rule and maps it to a corresponding operation in the verification framework. There is some additional complexity in this approach that we won't cover here in that often the order in which proof rules are applied in a verification framework doesn't exactly align with the order in which they occur during synthesis, but it turns out that we are able to handle this quite elegantly using a kind of deferred evaluation.
Using this methodology, we then are able to extend the existing SuSLik to produce fully certified programs, with associated Coq proof-scripts verified in 3 different separation logic frameworks:
- The Hoare Type Theory Coq Framework
- The Iris Coq Framework
- The Verified Software Toolchain (VST) Framework
Notably of which, the last one (VST), allows us to produce fully verified executable C code as an output from SuSLik.
Interested? Learn more…
That concludes the high level overview of this latest work and how exactly it works. Hopefully this has highlighted how surprisingly practical and extensible this approach to automated certified program synthesis can be, and potentially piqued your interest into this work. As usual, there have been many aspects of this work I have not mentioned here in the interests of providing an approachable overview, such as:
- complexities of handling the differences between a verification proof tree and synthesis proof tree
- the challenges of implementing a generic translator between 3 wildly different verification frameworks
- the various limitations of each of the different backends and the impacts these have on the types of programs that can and can't be certified.
If you are interested, I'd recommend checking out the full paper (see here), or checking out the presentation of this paper at ICFP later this year (to be announced).
The tool itself in this research project can be found on the certification branch of the SuSLik repository: https://github.com/TyGuS/suslik/tree/certification
Bibliography
- Project Repository
- "Structuring the Synthesis of Heap-Manipulating Programs" (POPL'19)
- "Certifying the Synthesis of Heap Manipulating Programs" (ICFP'21)
- Coq Proof Assistant
- Iris Coq Framework
- Verified Software Toolchain (VST) Framework
- Hoare Type Theory Coq Framework
- Separation logic
- Proof Carrying Code