Bloom filters debunked: Dispelling 30 Years of bad math with Coq!
#projects #research #coq #verificationIntroduction
There's this rather nifty feature of modern web browsers (such as Firefox or Chrome) where the browser will automatically warn the user if they happen to navigate to a "malicious" URL:
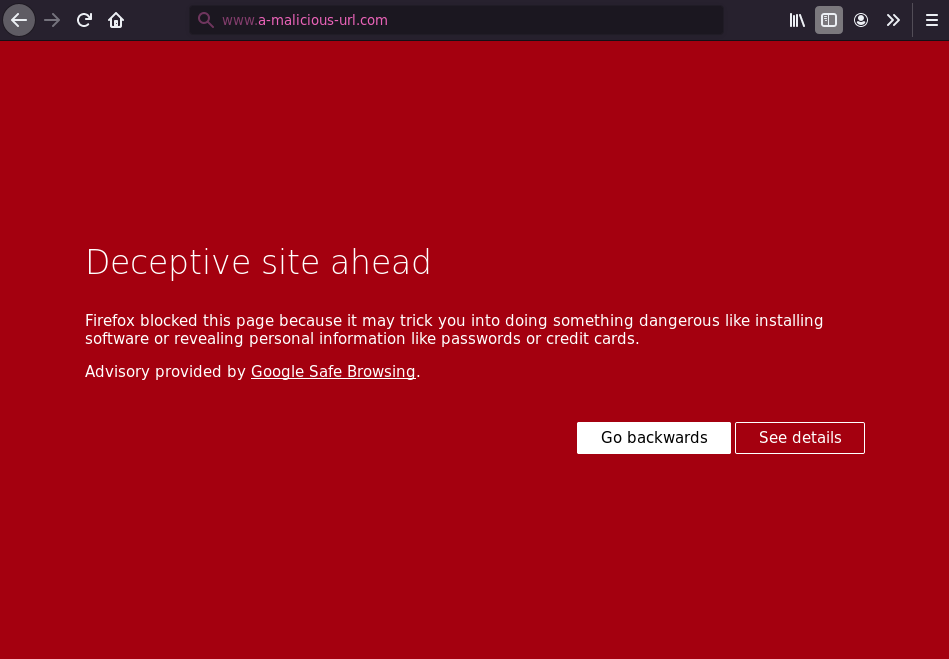
While conceptually simple, this feature actually requires more engineering effort than one would expect - in particular, tracking the set of known malicious URLs in a practical manner turns out to be somewhat difficult.
This is because, on one hand, trying to store the database of all known malicious URLs, which, bear in mind, may contain millions and millions of entries, is something that is just practically infeasible for most users.

Conversely, sending every URL that a user visits to some external service, where it could be logged and data-mined by nefarious third parties, is something that most users should probably not be comfortable with.
As it turns out, browsers actually implement this functionality by means of a rather interesting compromise1.
Using a probabilistic data structure known as a Bloom filter, Browsers maintain a approximate representation of the set of known malicious URLs locally. By querying this space-efficient local set, browsers will only send up a small proportion of the honest URLs.
This proxy technique, which safe-guards the privacy of millions of users ever day, depends on two key properties of Bloom filters:
- No false negatives
- This states that if a query for an URL in the Bloom filter returns negative, then the queried item can be guaranteed to not be present in the set of malicious URLs - i.e the Bloom filter is guaranteed to return a positive result for all known malicious URLs.
- Low false positive rate
- This property states that for any URL that is not in the set of malicious URLs, the likelihood of a Bloom filter query returning a positive result should be fairly low - thus minimising the number of unnecessary infractions on user privacy.
This mechanism works quite well, and the guarantees of a Bloom filter seem to be perfectly suited for this particular task, however it has one small problem, and that is:
In fact, as it turns out, the behaviours of a Bloom filter have actually been the subject of 30 years of mathematical contention, requiring multiple corrections and even corrections of these corrections.
Given this history of errors, can we really have any certainty in our understanding of a Bloom filter at all?
Well, never fear, I am writing this post to inform you that we have
just recently used Coq to produce the very first certified proof
of the false positive rate of a Bloom filter, finally putting an end to
this saga of errors and returning certainty (pardon the pun2) to a
mechanism that countless people rely on every single day.
In the rest of this post, we'll explore the main highlights of this research, answering the following questions:
- What is a Bloom filter?
- Why did these errors initially arise?
- What is the true behaviour of a Bloom filter? and how can we be certain?
This research was just recently presented at CAV2020 under the title "Certifying Certainty and Uncertainty in Approximate Membership Query Structures", you can find the paper here, and a video presentation of it here.
The code and proofs used in this research project are FOSS, and can be found on the Ceramist repo: https://github.com/certichain/ceramist
What is a Bloom filter?
So what exactly is a Bloom filter? and how exactly does it achieve these important properties?
Well, put simply, a Bloom filter 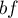 is a simply a combination of two
separate components:
is a simply a combination of two
separate components:
- A bit-vector of
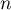 bits.
bits. - and a sequence of
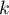 hash functions.
hash functions.
To use the Bloom filter as an approximate set, we can perform the standard set operations as follows:
- Insertion
- To insert a value
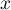 into a Bloom filter
into a Bloom filter 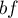 , simply
hash it over each one of the
, simply
hash it over each one of the 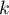 hash functions, and
treating the hash outputs as indices into the
bit-vector, raise the corresponding bits.
hash functions, and
treating the hash outputs as indices into the
bit-vector, raise the corresponding bits. - Query
- To query for a value
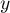 in the Bloom filter, once again
hash it over each one of the
in the Bloom filter, once again
hash it over each one of the 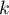 hash functions, and then
check whether all of the corresponding bits are raised.
hash functions, and then
check whether all of the corresponding bits are raised.
These operations, while fairly straightforward, are actually entirely sufficient to ensure the No false negatives property (see here for Coq statement):
When an item is inserted into the Bloom filter, it will result in a certain subset of the bits in the bit-vector being raised. As there are no operations that can unset these bits, we can be certain that any subsequent query for the inserted element must return true. In other words, if we get a negative result for a query, we can be certain that the item has never been inserted into the Bloom filter before.
This is the case for negative results; things get slightly more interesting for positive results due to the possibility of false positives.
To see how this may occur, consider the following scenario:
- Suppose we insert a value
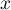 into a Bloom filter
into a Bloom filter 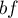 :
:
![\begin{tikzfigure*}
\begin{tikzpicture}[every path/.style={line width=1.75mm, >=stealth}]
\draw[fill=orange!50,draw=none] ($(-8.0, -1.0) + (0.0, -6.0) + (0.0, 0.0)$) rectangle ($(-6.0, 1.0) + (0.0, -6.0) + (0.0, 0.0)$);
\draw[fill=orange!50,draw=none] ($(-8.0, -1.0) + (0.0, -6.0) + (4.0, 0.0)$) rectangle ($(-6.0, 1.0) + (0.0, -6.0) + (4.0, 0.0)$);
\draw[fill=orange!50,draw=none] ($(-8.0, -1.0) + (0.0, -6.0) + (12.0, 0.0)$) rectangle ($(-6.0, 1.0) + (0.0, -6.0) + (12.0, 0.0)$);
\draw[fill=orange!50,draw=none] ($(-8.0, -1.0) + (0.0, -6.0) + (14.0, 0.0)$) rectangle ($(-6.0, 1.0) + (0.0, -6.0) + (14.0, 0.0)$);
\draw[fill=orange!20] ($(5.0, 1.0)$) rectangle ($(-5.0, -1.0)$);
\draw ($(-5.0, 1.0) + (2.0, 0.0)$) -- ($(-5.0, -1.0) + (2.0, 0.0)$)
($(-5.0, 1.0) + (4.0, 0.0)$) -- ($(-5.0, -1.0) + (4.0, 0.0)$)
($(-5.0, 1.0) + (6.0, 0.0)$) -- ($(-5.0, -1.0) + (6.0, 0.0)$)
($(-5.0, 1.0) + (8.0, 0.0)$) -- ($(-5.0, -1.0) + (8.0, 0.0)$);
\draw ($(8.0, 1.0) + (0.0, -6.0)$) rectangle ($(-8.0, -1.0) + (0.0, -6.0)$);
\draw ($(-8.0, 1.0) + (0.0, -6.0) + (2.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (2.0, 0.0)$)
($(-8.0, 1.0) + (0.0, -6.0) + (4.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (4.0, 0.0)$)
($(-8.0, 1.0) + (0.0, -6.0) + (6.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (6.0, 0.0)$)
($(-8.0, 1.0) + (0.0, -6.0) + (8.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (8.0, 0.0)$)
($(-8.0, 1.0) + (0.0, -6.0) + (10.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (10.0, 0.0)$)
($(-8.0, 1.0) + (0.0, -6.0) + (12.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (12.0, 0.0)$)
($(-8.0, 1.0) + (0.0, -6.0) + (14.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (14.0, 0.0)$);
\node (x) at (0.0, 4.0) {\fontsize{38}{38}\selectfont x};
\draw[->] ($(x) + (0.0, -1.0)$) -- ($(-4.0, 1.25) + (0.0, 0.0)$);
\draw[->] ($(x) + (0.0, -1.0)$) -- ($(-4.0, 1.25) + (2.0, 0.0)$);
\draw[->] ($(x) + (0.0, -1.0)$) -- ($(-4.0, 1.25) + (4.0, 0.0)$);
\draw[->] ($(x) + (0.0, -1.0)$) -- ($(-4.0, 1.25) + (6.0, 0.0)$);
\draw[->] ($(x) + (0.0, -1.0)$) -- ($(-4.0, 1.25) + (8.0, 0.0)$);
\draw[->] ($(-4.0, -1.25) + (0.0, 0.0)$) to[in=80, out=200] ($(-7.0, 1.25) + (0.0, -6.0) + (0.0, 0.0)$) ;
\draw[->] ($(-4.0, -1.25) + (2.0, 0.0)$) to[in=140, out=-90] ($(-7.0, 1.25) + (0.0, -6.0) + (12.0, 0.0)$) ;
\draw[->] ($(-4.0, -1.25) + (4.0, 0.0)$) to[in=90, out=-90] ($(-7.0, 1.25) + (0.0, -6.0) + (14.0, 0.0)$);
\draw[->] ($(-4.0, -1.25) + (6.0, 0.0)$) to[in=80, out=-90] ($(-7.0, 1.25) + (0.0, -6.0) + (4.0, 0.0)$);
\draw[->] ($(-4.0, -1.25) + (8.0, 0.0)$) to[in=80, out=-30] ($(-7.0, 1.25) + (0.0, -6.0) + (14.0, 0.0)$);
\node at ($(-4.0, 0.0) + (0.0, 0.0)$) {\fontsize{30}{38}\selectfont $h_1$};
\node at ($(-4.0, 0.0) + (2.0, 0.0)$) {\fontsize{30}{38}\selectfont $h_2$};
\node at ($(-4.0, 0.0) + (4.0, 0.0)$) {\fontsize{30}{38}\selectfont $h_3$};
\node at ($(-4.0, 0.0) + (6.0, 0.0)$) {\fontsize{30}{38}\selectfont $h_4$};
\node at ($(-4.0, 0.0) + (8.0, 0.0)$) {\fontsize{30}{38}\selectfont $h_5$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (0.0, 0.0)$) {\fontsize{30}{38}\selectfont $b_1$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (2.0, 0.0)$) {\fontsize{30}{38}\selectfont $b_2$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (4.0, 0.0)$) {\fontsize{30}{38}\selectfont $b_3$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (6.0, 0.0)$) {\fontsize{30}{38}\selectfont $b_4$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (8.0, 0.0)$) {\fontsize{30}{38}\selectfont $b_5$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (10.0, 0.0)$) {\fontsize{30}{38}\selectfont $b_6$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (12.0, 0.0)$) {\fontsize{30}{38}\selectfont $b_7$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (14.0, 0.0)$) {\fontsize{30}{38}\selectfont $b_8$};
\end{tikzpicture}
\end{tikzfigure*}](../images/latex/log-bloomfilters-debunked_ddfaf5db5b344bb072d88058f06e365ed574a490.png) 1
1
- Inserting this value will thus result in a subset of the bits in the bit-vector being raised.
- At a later point, we may choose to query the Bloom filter for a
different value
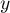 .
. - Depending on the choice of hash functions, there is a possibility
that the corresponding set of bits that
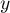 maps to will be a subset
of those that are already raised.
maps to will be a subset
of those that are already raised.
![\begin{tikzfigure*}
\begin{tikzpicture}[every path/.style={line width=1.75mm, >=stealth}]
\draw[fill=orange!50,draw=none] ($(-8.0, -1.0) + (0.0, -6.0) + (0.0, 0.0)$) rectangle ($(-6.0, 1.0) + (0.0, -6.0) + (0.0, 0.0)$);
\draw[fill=orange!50,draw=none] ($(-8.0, -1.0) + (0.0, -6.0) + (4.0, 0.0)$) rectangle ($(-6.0, 1.0) + (0.0, -6.0) + (4.0, 0.0)$);
\draw[fill=orange!50,draw=none] ($(-8.0, -1.0) + (0.0, -6.0) + (12.0, 0.0)$) rectangle ($(-6.0, 1.0) + (0.0, -6.0) + (12.0, 0.0)$);
\draw[fill=orange!50,draw=none] ($(-8.0, -1.0) + (0.0, -6.0) + (14.0, 0.0)$) rectangle ($(-6.0, 1.0) + (0.0, -6.0) + (14.0, 0.0)$);
\draw[fill=orange!20] ($(5.0, 1.0)$) rectangle ($(-5.0, -1.0)$);
\draw ($(-5.0, 1.0) + (2.0, 0.0)$) -- ($(-5.0, -1.0) + (2.0, 0.0)$)
($(-5.0, 1.0) + (4.0, 0.0)$) -- ($(-5.0, -1.0) + (4.0, 0.0)$)
($(-5.0, 1.0) + (6.0, 0.0)$) -- ($(-5.0, -1.0) + (6.0, 0.0)$)
($(-5.0, 1.0) + (8.0, 0.0)$) -- ($(-5.0, -1.0) + (8.0, 0.0)$);
\draw ($(8.0, 1.0) + (0.0, -6.0)$) rectangle ($(-8.0, -1.0) + (0.0, -6.0)$);
\draw ($(-8.0, 1.0) + (0.0, -6.0) + (2.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (2.0, 0.0)$)
($(-8.0, 1.0) + (0.0, -6.0) + (4.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (4.0, 0.0)$)
($(-8.0, 1.0) + (0.0, -6.0) + (6.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (6.0, 0.0)$)
($(-8.0, 1.0) + (0.0, -6.0) + (8.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (8.0, 0.0)$)
($(-8.0, 1.0) + (0.0, -6.0) + (10.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (10.0, 0.0)$)
($(-8.0, 1.0) + (0.0, -6.0) + (12.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (12.0, 0.0)$)
($(-8.0, 1.0) + (0.0, -6.0) + (14.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (14.0, 0.0)$);
\node (x) at (0.0, 4.0) {\fontsize{38}{38}\selectfont y?};
\draw[->] ($(x) + (0.0, -1.0)$) -- ($(-4.0, 1.25) + (0.0, 0.0)$);
\draw[->] ($(x) + (0.0, -1.0)$) -- ($(-4.0, 1.25) + (2.0, 0.0)$);
\draw[->] ($(x) + (0.0, -1.0)$) -- ($(-4.0, 1.25) + (4.0, 0.0)$);
\draw[->] ($(x) + (0.0, -1.0)$) -- ($(-4.0, 1.25) + (6.0, 0.0)$);
\draw[->] ($(x) + (0.0, -1.0)$) -- ($(-4.0, 1.25) + (8.0, 0.0)$);
\draw[->] ($(-4.0, -1.25) + (0.0, 0.0)$) to[in=80, out=200] ($(-7.0, 1.25) + (0.0, -6.0) + (0.0, 0.0)$) ;
\draw[->] ($(-4.0, -1.25) + (2.0, 0.0)$) to[in=120, out=-90] ($(-7.0, 1.25) + (0.0, -6.0) + (12.0, 0.0)$) ;
\draw[->] ($(-4.0, -1.25) + (4.0, 0.0)$) to[in=90, out=-90] ($(-7.0, 1.25) + (0.0, -6.0) + (12.0, 0.0)$);
\draw[->] ($(-4.0, -1.25) + (6.0, 0.0)$) to[in=60, out=-90] ($(-7.0, 1.25) + (0.0, -6.0) + (0.0, 0.0)$);
\draw[->] ($(-4.0, -1.25) + (8.0, 0.0)$) to[in=90, out=-90] ($(-7.0, 1.25) + (0.0, -6.0) + (12.0, 0.0)$);
\node at ($(-4.0, 0.0) + (0.0, 0.0)$) {\fontsize{30}{38}\selectfont $h_1$};
\node at ($(-4.0, 0.0) + (2.0, 0.0)$) {\fontsize{30}{38}\selectfont $h_2$};
\node at ($(-4.0, 0.0) + (4.0, 0.0)$) {\fontsize{30}{38}\selectfont $h_3$};
\node at ($(-4.0, 0.0) + (6.0, 0.0)$) {\fontsize{30}{38}\selectfont $h_4$};
\node at ($(-4.0, 0.0) + (8.0, 0.0)$) {\fontsize{30}{38}\selectfont $h_5$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (0.0, 0.0)$) {\fontsize{30}{38}\selectfont $b_1$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (2.0, 0.0)$) {\fontsize{30}{38}\selectfont $b_2$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (4.0, 0.0)$) {\fontsize{30}{38}\selectfont $b_3$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (6.0, 0.0)$) {\fontsize{30}{38}\selectfont $b_4$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (8.0, 0.0)$) {\fontsize{30}{38}\selectfont $b_5$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (10.0, 0.0)$) {\fontsize{30}{38}\selectfont $b_6$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (12.0, 0.0)$) {\fontsize{30}{38}\selectfont $b_7$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (14.0, 0.0)$) {\fontsize{30}{38}\selectfont $b_8$};
\end{tikzpicture}
\end{tikzfigure*}](../images/latex/log-bloomfilters-debunked_c3010e84fac418377bffc319e5a67d05b074e688.png) 1
1
- In this case, our query would return a positive result even though
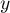 is not actually in the Bloom filter.
is not actually in the Bloom filter.
Ideally, we'd like to characterise the frequency at which these kinds of results may occur, however this will generally be highly dependent on the particular choice of hash functions, limiting the scope of our analysis.
As is the standard approach for these kinds of data structures, in order to get a more general result, we can instead treat the hash functions and their outputs as random (more on this later).
With this modelling assumption, the property of interest now becomes the False positive probability - that is:
- False positive probability
- After inserting
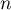 elements into an
empty Bloom filter
elements into an
empty Bloom filter 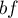 , the probability that querying for an
unseen value
, the probability that querying for an
unseen value 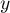 returns a positive result.
returns a positive result.
As part of the analysis accompanying the original description of the Bloom filter (by Burton Howard Bloom in 1970), Bloom provides a derivation for the false positive rate.
Bloom's Analysis
Note: The analysis used by Bloom in his original paper actually uses a slightly different definition of a Bloomfilter than the one that is typically used (Bloom assumes that the hash functions are distinct, which is typically hard to achieve in practice) - I present the following as being "Bloom's" analysis to follow the narrative, but in fact this proof is based on the Knuth's variant of the Bloomfilter, so Bloom is not the one who originally introduced the error.
Bloom proposes we begin the analysis by focusing on the behaviours of
an arbitrary single bit of the bit-vector, and then generalise the
result at the end - for the purposes of illustration, suppose that
this bit is 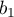 .
.
![\begin{tikzfigure*}
\begin{tikzpicture}[scale=0.45,every path/.style={line width=0.75mm, >=stealth}]
\draw[fill=orange!20] ($(5.0, 1.0)$) rectangle ($(-5.0, -1.0)$);
\draw ($(-5.0, 1.0) + (2.0, 0.0)$) -- ($(-5.0, -1.0) + (2.0, 0.0)$) ($(-5.0, 1.0) + (4.0, 0.0)$) -- ($(-5.0, -1.0) + (4.0, 0.0)$) ($(-5.0, 1.0) + (6.0, 0.0)$) -- ($(-5.0, -1.0) + (6.0, 0.0)$) ($(-5.0, 1.0) + (8.0, 0.0)$) -- ($(-5.0, -1.0) + (8.0, 0.0)$);
\draw ($(8.0, 1.0) + (0.0, -6.0)$) rectangle ($(-8.0, -1.0) + (0.0, -6.0)$);
\draw ($(-8.0, 1.0) + (0.0, -6.0) + (2.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (2.0, 0.0)$) ($(-8.0, 1.0) + (0.0, -6.0) + (4.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (4.0, 0.0)$) ($(-8.0, 1.0) + (0.0, -6.0) + (6.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (6.0, 0.0)$) ($(-8.0, 1.0) + (0.0, -6.0) + (8.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (8.0, 0.0)$) ($(-8.0, 1.0) + (0.0, -6.0) + (10.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (10.0, 0.0)$) ($(-8.0, 1.0) + (0.0, -6.0) + (12.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (12.0, 0.0)$) ($(-8.0, 1.0) + (0.0, -6.0) + (14.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (14.0, 0.0)$);
\node (x) at (0.0, 4.0) {\fontsize{28}{28}\selectfont $x_1$};
\node (dots) at (2.0, 4.0) {\fontsize{18}{28}\selectfont $\dots$};
\node (xn) at (4.0, 4.0) {\fontsize{28}{28}\selectfont $x_n$};
\draw[->, line width=1mm,draw=orange] ($(-7.0, 1.25) + (0.0, -10.0) + (0.0, 0.0)$) -- ($(-7.0, 1.25) + (0.0, -8.0) + (0.0, 0.0)$);
\node at ($(-4.0, 0.0) + (0.0, 0.0)$) {\fontsize{20}{38}\selectfont $h_1$};
\node at ($(-4.0, 0.0) + (2.0, 0.0)$) {\fontsize{20}{38}\selectfont $h_2$};
\node at ($(-4.0, 0.0) + (4.0, 0.0)$) {\fontsize{20}{38}\selectfont $h_3$};
\node at ($(-4.0, 0.0) + (6.0, 0.0)$) {\fontsize{12}{38}\selectfont $\dots$};
\node at ($(-4.0, 0.0) + (8.0, 0.0)$) {\fontsize{20}{38}\selectfont $h_k$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (0.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_1$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (2.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_2$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (4.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_3$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (6.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_4$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (8.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_5$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (10.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_6$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (12.0, 0.0)$) {\fontsize{12}{38}\selectfont $\dots$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (14.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_m$};
\end{tikzpicture}
\end{tikzfigure*}](../images/latex/log-bloomfilters-debunked_c158fc886d810a61b28b8748050605361f4a6247.png) 1
1
Now, let's have a look at what happens when we hash an input over one of the hash functions in the Bloom filter.
![\begin{tikzfigure*}
\begin{tikzpicture}[scale=0.45,every path/.style={line width=0.75mm, >=stealth}]
\draw[fill=orange!20] ($(5.0, 1.0)$) rectangle ($(-5.0, -1.0)$);
\draw ($(-5.0, 1.0) + (2.0, 0.0)$) -- ($(-5.0, -1.0) + (2.0, 0.0)$) ($(-5.0, 1.0) + (4.0, 0.0)$) -- ($(-5.0, -1.0) + (4.0, 0.0)$) ($(-5.0, 1.0) + (6.0, 0.0)$) -- ($(-5.0, -1.0) + (6.0, 0.0)$) ($(-5.0, 1.0) + (8.0, 0.0)$) -- ($(-5.0, -1.0) + (8.0, 0.0)$);
\node (x) at (0.0, 4.0) {\fontsize{28}{28}\selectfont $x_1$};
\node (dots) at (2.0, 4.0) {\fontsize{18}{28}\selectfont $\dots$};
\node (xn) at (4.0, 4.0) {\fontsize{28}{28}\selectfont $x_n$};
\draw[->] ($(x) + (0.0, -1.0)$) -- ($(-4.0, 1.25) + (0.0, 0.0)$);
\node at ($(-4.0, 0.0) + (0.0, 0.0)$) {\fontsize{20}{38}\selectfont $h_1$};
\node at ($(-4.0, 0.0) + (2.0, 0.0)$) {\fontsize{20}{38}\selectfont $h_2$};
\node at ($(-4.0, 0.0) + (4.0, 0.0)$) {\fontsize{20}{38}\selectfont $h_3$};
\node at ($(-4.0, 0.0) + (6.0, 0.0)$) {\fontsize{12}{38}\selectfont $\dots$};
\node at ($(-4.0, 0.0) + (8.0, 0.0)$) {\fontsize{20}{38}\selectfont $h_k$};
\end{tikzpicture}
\end{tikzfigure*}](../images/latex/log-bloomfilters-debunked_d46ab5f330eaaf9aa4cbb14657982350085b263c.png) 1
1
As we're treating the hash functions as random, the hash outputs can be thought of as being uniformly randomly distributed over each possible bit.
![\begin{tikzfigure*}
\begin{tikzpicture}[scale=0.45,every path/.style={line width=0.75mm, >=stealth}]
\draw[fill=orange!20] ($(5.0, 1.0)$) rectangle ($(-5.0, -1.0)$);
\draw ($(-5.0, 1.0) + (2.0, 0.0)$) -- ($(-5.0, -1.0) + (2.0, 0.0)$) ($(-5.0, 1.0) + (4.0, 0.0)$) -- ($(-5.0, -1.0) + (4.0, 0.0)$) ($(-5.0, 1.0) + (6.0, 0.0)$) -- ($(-5.0, -1.0) + (6.0, 0.0)$) ($(-5.0, 1.0) + (8.0, 0.0)$) -- ($(-5.0, -1.0) + (8.0, 0.0)$);
\draw ($(8.0, 1.0) + (0.0, -6.0)$) rectangle ($(-8.0, -1.0) + (0.0, -6.0)$);
\draw ($(-8.0, 1.0) + (0.0, -6.0) + (2.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (2.0, 0.0)$) ($(-8.0, 1.0) + (0.0, -6.0) + (4.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (4.0, 0.0)$) ($(-8.0, 1.0) + (0.0, -6.0) + (6.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (6.0, 0.0)$) ($(-8.0, 1.0) + (0.0, -6.0) + (8.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (8.0, 0.0)$) ($(-8.0, 1.0) + (0.0, -6.0) + (10.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (10.0, 0.0)$) ($(-8.0, 1.0) + (0.0, -6.0) + (12.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (12.0, 0.0)$) ($(-8.0, 1.0) + (0.0, -6.0) + (14.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (14.0, 0.0)$);
\node (x) at (0.0, 4.0) {\fontsize{28}{28}\selectfont $x_1$};
\node (dots) at (2.0, 4.0) {\fontsize{18}{28}\selectfont $\dots$};
\node (xn) at (4.0, 4.0) {\fontsize{28}{28}\selectfont $x_n$};
\draw[->, line width=1mm,draw=orange] ($(-7.0, 1.25) + (0.0, -10.0) + (0.0, 0.0)$) -- ($(-7.0, 1.25) + (0.0, -8.0) + (0.0, 0.0)$);
\draw[->] ($(x) + (0.0, -1.0)$) -- ($(-4.0, 1.25) + (0.0, 0.0)$);
\draw[->] ($(-4.0, -1.25) + (0.0, 0.0)$) to[in=80, out=200] ($(-7.0, 1.25) + (0.0, -6.0) + (0.0, 0.0)$);
\node at ($(-4.0, 0.0) + (0.0, 0.0)$) {\fontsize{20}{38}\selectfont $h_1$};
\node at ($(-4.0, 0.0) + (2.0, 0.0)$) {\fontsize{20}{38}\selectfont $h_2$};
\node at ($(-4.0, 0.0) + (4.0, 0.0)$) {\fontsize{20}{38}\selectfont $h_3$};
\node at ($(-4.0, 0.0) + (6.0, 0.0)$) {\fontsize{12}{38}\selectfont $\dots$};
\node at ($(-4.0, 0.0) + (8.0, 0.0)$) {\fontsize{20}{38}\selectfont $h_k$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (0.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_1$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (2.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_2$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (4.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_3$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (6.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_4$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (8.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_5$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (10.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_6$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (12.0, 0.0)$) {\fontsize{12}{38}\selectfont $\dots$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (14.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_m$};
\end{tikzpicture}
\end{tikzfigure*}](../images/latex/log-bloomfilters-debunked_13fffe8d823b86a5cdb6b2708059e95db39d8ab2.png) 1
1
As such, the probability that the hash function happens to hit our
selected bit will simply be - 1 over the number of bits -  .
Obviously, this naturally also means the probability that the hash output
misses our selected bit will just be
.
Obviously, this naturally also means the probability that the hash output
misses our selected bit will just be  .
.
![\begin{tikzfigure*}
\begin{tikzpicture}[scale=0.45,every path/.style={line width=0.75mm, >=stealth}]
\draw[fill=orange!50,draw=none] ($(-8.0, -1.0) + (0.0, -6.0) + (6.0, 0.0)$) rectangle ($(-6.0, 1.0) + (0.0, -6.0) + (6.0, 0.0)$);
\draw[fill=orange!20] ($(5.0, 1.0)$) rectangle ($(-5.0, -1.0)$);
\draw ($(-5.0, 1.0) + (2.0, 0.0)$) -- ($(-5.0, -1.0) + (2.0, 0.0)$) ($(-5.0, 1.0) + (4.0, 0.0)$) -- ($(-5.0, -1.0) + (4.0, 0.0)$) ($(-5.0, 1.0) + (6.0, 0.0)$) -- ($(-5.0, -1.0) + (6.0, 0.0)$) ($(-5.0, 1.0) + (8.0, 0.0)$) -- ($(-5.0, -1.0) + (8.0, 0.0)$);
\draw ($(8.0, 1.0) + (0.0, -6.0)$) rectangle ($(-8.0, -1.0) + (0.0, -6.0)$);
\draw ($(-8.0, 1.0) + (0.0, -6.0) + (2.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (2.0, 0.0)$) ($(-8.0, 1.0) + (0.0, -6.0) + (4.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (4.0, 0.0)$) ($(-8.0, 1.0) + (0.0, -6.0) + (6.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (6.0, 0.0)$) ($(-8.0, 1.0) + (0.0, -6.0) + (8.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (8.0, 0.0)$) ($(-8.0, 1.0) + (0.0, -6.0) + (10.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (10.0, 0.0)$) ($(-8.0, 1.0) + (0.0, -6.0) + (12.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (12.0, 0.0)$) ($(-8.0, 1.0) + (0.0, -6.0) + (14.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (14.0, 0.0)$);
\node (x) at (0.0, 4.0) {\fontsize{28}{28}\selectfont $x_1$};
\node (dots) at (2.0, 4.0) {\fontsize{18}{28}\selectfont $\dots$};
\node (xn) at (4.0, 4.0) {\fontsize{28}{28}\selectfont $x_n$};
\draw[->, line width=1mm,draw=orange] ($(-7.0, 1.25) + (0.0, -10.0) + (0.0, 0.0)$) -- ($(-7.0, 1.25) + (0.0, -8.0) + (0.0, 0.0)$);
\draw[->] ($(x) + (0.0, -1.0)$) -- ($(-4.0, 1.25) + (0.0, 0.0)$);
\draw[->] ($(-4.0, -1.25) + (0.0, 0.0)$) to[in=130, out=-90] ($(-7.0, 1.25) + (0.0, -6.0) + (6.0, 0.0)$);
\node at ($(-4.0, 0.0) + (0.0, 0.0)$) {\fontsize{20}{38}\selectfont $h_1$};
\node at ($(-4.0, 0.0) + (2.0, 0.0)$) {\fontsize{20}{38}\selectfont $h_2$};
\node at ($(-4.0, 0.0) + (4.0, 0.0)$) {\fontsize{20}{38}\selectfont $h_3$};
\node at ($(-4.0, 0.0) + (6.0, 0.0)$) {\fontsize{12}{38}\selectfont $\dots$};
\node at ($(-4.0, 0.0) + (8.0, 0.0)$) {\fontsize{20}{38}\selectfont $h_k$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (0.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_1$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (2.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_2$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (4.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_3$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (6.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_4$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (8.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_5$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (10.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_6$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (12.0, 0.0)$) {\fontsize{12}{38}\selectfont $\dots$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (14.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_m$};
\end{tikzpicture}
\end{tikzfigure*}](../images/latex/log-bloomfilters-debunked_ecabde25c0731be772310c5515c641955c56d4fa.png) 1
1
From here, as all the hash functions are also independent, this means
that the probability that our selected bit remains unset, even after
executing all the 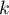 hash functions, will be
hash functions, will be 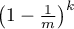 .
.
![\begin{tikzfigure*}
\begin{tikzpicture}[scale=0.45,every path/.style={line width=0.75mm, >=stealth}]
\draw[fill=orange!50,draw=none] ($(-8.0, -1.0) + (0.0, -6.0) + (4.0, 0.0)$) rectangle ($(-6.0, 1.0) + (0.0, -6.0) + (4.0, 0.0)$);
\draw[fill=orange!50,draw=none] ($(-8.0, -1.0) + (0.0, -6.0) + (6.0, 0.0)$) rectangle ($(-6.0, 1.0) + (0.0, -6.0) + (6.0, 0.0)$);
\draw[fill=orange!50,draw=none] ($(-8.0, -1.0) + (0.0, -6.0) + (12.0, 0.0)$) rectangle ($(-6.0, 1.0) + (0.0, -6.0) + (12.0, 0.0)$);
\draw[fill=orange!50,draw=none] ($(-8.0, -1.0) + (0.0, -6.0) + (14.0, 0.0)$) rectangle ($(-6.0, 1.0) + (0.0, -6.0) + (14.0, 0.0)$);
\draw[fill=orange!20] ($(5.0, 1.0)$) rectangle ($(-5.0, -1.0)$);
\draw ($(-5.0, 1.0) + (2.0, 0.0)$) -- ($(-5.0, -1.0) + (2.0, 0.0)$) ($(-5.0, 1.0) + (4.0, 0.0)$) -- ($(-5.0, -1.0) + (4.0, 0.0)$) ($(-5.0, 1.0) + (6.0, 0.0)$) -- ($(-5.0, -1.0) + (6.0, 0.0)$) ($(-5.0, 1.0) + (8.0, 0.0)$) -- ($(-5.0, -1.0) + (8.0, 0.0)$);
\draw ($(8.0, 1.0) + (0.0, -6.0)$) rectangle ($(-8.0, -1.0) + (0.0, -6.0)$);
\draw ($(-8.0, 1.0) + (0.0, -6.0) + (2.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (2.0, 0.0)$) ($(-8.0, 1.0) + (0.0, -6.0) + (4.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (4.0, 0.0)$) ($(-8.0, 1.0) + (0.0, -6.0) + (6.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (6.0, 0.0)$) ($(-8.0, 1.0) + (0.0, -6.0) + (8.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (8.0, 0.0)$) ($(-8.0, 1.0) + (0.0, -6.0) + (10.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (10.0, 0.0)$) ($(-8.0, 1.0) + (0.0, -6.0) + (12.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (12.0, 0.0)$) ($(-8.0, 1.0) + (0.0, -6.0) + (14.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (14.0, 0.0)$);
\node (x) at (0.0, 4.0) {\fontsize{28}{28}\selectfont $x_1$};
\node (dots) at (2.0, 4.0) {\fontsize{18}{28}\selectfont $\dots$};
\node (xn) at (4.0, 4.0) {\fontsize{28}{28}\selectfont $x_n$};
\draw[->, line width=1mm,draw=orange] ($(-7.0, 1.25) + (0.0, -10.0) + (0.0, 0.0)$) -- ($(-7.0, 1.25) + (0.0, -8.0) + (0.0, 0.0)$);
\draw[->] ($(x) + (0.0, -1.0)$) -- ($(-4.0, 1.25) + (0.0, 0.0)$);
\draw[->] ($(x) + (0.0, -1.0)$) -- ($(-4.0, 1.25) + (2.0, 0.0)$);
\draw[->] ($(x) + (0.0, -1.0)$) -- ($(-4.0, 1.25) + (4.0, 0.0)$);
\draw[->] ($(x) + (0.0, -1.0)$) -- ($(-4.0, 1.25) + (6.0, 0.0)$);
\draw[->] ($(x) + (0.0, -1.0)$) -- ($(-4.0, 1.25) + (8.0, 0.0)$);
\draw[->] ($(-4.0, -1.25) + (0.0, 0.0)$) to[in=130, out=-90] ($(-7.0, 1.25) + (0.0, -6.0) + (6.0, 0.0)$);
\draw[->] ($(-4.0, -1.25) + (2.0, 0.0)$) to[in=140, out=-90] ($(-7.0, 1.25) + (0.0, -6.0) + (12.0, 0.0)$) ;
\draw[->] ($(-4.0, -1.25) + (4.0, 0.0)$) to[in=90, out=-90] ($(-7.0, 1.25) + (0.0, -6.0) + (14.0, 0.0)$);
\draw[->] ($(-4.0, -1.25) + (6.0, 0.0)$) to[in=80, out=-90] ($(-7.0, 1.25) + (0.0, -6.0) + (4.0, 0.0)$);
\draw[->] ($(-4.0, -1.25) + (8.0, 0.0)$) to[in=80, out=-30] ($(-7.0, 1.25) + (0.0, -6.0) + (14.0, 0.0)$);
\node at ($(-4.0, 0.0) + (0.0, 0.0)$) {\fontsize{20}{38}\selectfont $h_1$};
\node at ($(-4.0, 0.0) + (2.0, 0.0)$) {\fontsize{20}{38}\selectfont $h_2$};
\node at ($(-4.0, 0.0) + (4.0, 0.0)$) {\fontsize{20}{38}\selectfont $h_3$};
\node at ($(-4.0, 0.0) + (6.0, 0.0)$) {\fontsize{12}{38}\selectfont $\dots$};
\node at ($(-4.0, 0.0) + (8.0, 0.0)$) {\fontsize{20}{38}\selectfont $h_k$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (0.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_1$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (2.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_2$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (4.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_3$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (6.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_4$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (8.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_5$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (10.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_6$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (12.0, 0.0)$) {\fontsize{12}{38}\selectfont $\dots$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (14.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_m$};
\end{tikzpicture}
\end{tikzfigure*}](../images/latex/log-bloomfilters-debunked_9bd324bffd395aba981f80c63d4c90abdf7b54d0.png) 1
1
In fact, provided that the list of elements to be inserted is unique,
this independence argument actually generalises over all the hash
invocations, and thus we can conclude that the probability that our
selected bit is not raised during the execution will be 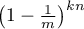 .
.
Inverting this expression, we derive that the probability that an
arbitrary bit in the bit-vector is raised after inserting 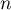 elements
will simply be
elements
will simply be 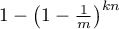 .
.
![\begin{tikzfigure*}
\begin{tikzpicture}[scale=0.45,every path/.style={line width=0.75mm, >=stealth}]
\draw[fill=orange!50,draw=none] ($(-8.0, -1.0) + (0.0, -6.0) + (0.0, 0.0)$) rectangle ($(-6.0, 1.0) + (0.0, -6.0) + (0.0, 0.0)$);
\draw ($(8.0, 1.0) + (0.0, -6.0)$) rectangle ($(-8.0, -1.0) + (0.0, -6.0)$);
\draw ($(-8.0, 1.0) + (0.0, -6.0) + (2.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (2.0, 0.0)$) ($(-8.0, 1.0) + (0.0, -6.0) + (4.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (4.0, 0.0)$) ($(-8.0, 1.0) + (0.0, -6.0) + (6.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (6.0, 0.0)$) ($(-8.0, 1.0) + (0.0, -6.0) + (8.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (8.0, 0.0)$) ($(-8.0, 1.0) + (0.0, -6.0) + (10.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (10.0, 0.0)$) ($(-8.0, 1.0) + (0.0, -6.0) + (12.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (12.0, 0.0)$) ($(-8.0, 1.0) + (0.0, -6.0) + (14.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (14.0, 0.0)$);
\draw[->, line width=1mm,draw=orange] ($(-7.0, 1.25) + (0.0, -10.0) + (0.0, 0.0)$) -- ($(-7.0, 1.25) + (0.0, -8.0) + (0.0, 0.0)$);
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (0.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_1$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (2.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_2$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (4.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_3$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (6.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_4$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (8.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_5$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (10.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_6$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (12.0, 0.0)$) {\fontsize{12}{38}\selectfont $\dots$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (14.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_m$};
\end{tikzpicture}
\end{tikzfigure*}](../images/latex/log-bloomfilters-debunked_d5d51803b5c7b5687e7dfb91aa86e44eb2e45455.png) 1
1
So far this derivation is entirely correct - this expression we have proven is actually correct (see here for a corresponding Coq proof), but it only applies for a single bit not a false positive result.
In order to generalise this result, Bloom then reasons that we can
interpret the occurrence of a false-positive result as being
equivalent to each of the 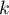 bits selected by the hash functions
being raised.
bits selected by the hash functions
being raised.
![\begin{tikzfigure*}
\begin{tikzpicture}[scale=0.45,every path/.style={line width=0.75mm, >=stealth}]
\draw[fill=orange!50,draw=none] ($(-8.0, -1.0) + (0.0, -6.0) + (0.0, 0.0)$) rectangle ($(-6.0, 1.0) + (0.0, -6.0) + (0.0, 0.0)$);
\draw[fill=orange!50,draw=none] ($(-8.0, -1.0) + (0.0, -6.0) + (4.0, 0.0)$) rectangle ($(-6.0, 1.0) + (0.0, -6.0) + (4.0, 0.0)$);
\draw[fill=orange!50,draw=none] ($(-8.0, -1.0) + (0.0, -6.0) + (10.0, 0.0)$) rectangle ($(-6.0, 1.0) + (0.0, -6.0) + (10.0, 0.0)$);
\draw[fill=orange!50,draw=none] ($(-8.0, -1.0) + (0.0, -6.0) + (12.0, 0.0)$) rectangle ($(-6.0, 1.0) + (0.0, -6.0) + (12.0, 0.0)$);
\draw[fill=orange!50,draw=none] ($(-8.0, -1.0) + (0.0, -6.0) + (14.0, 0.0)$) rectangle ($(-6.0, 1.0) + (0.0, -6.0) + (14.0, 0.0)$);
\draw[fill=orange!20] ($(5.0, 1.0)$) rectangle ($(-5.0, -1.0)$);
\draw ($(-5.0, 1.0) + (2.0, 0.0)$) -- ($(-5.0, -1.0) + (2.0, 0.0)$) ($(-5.0, 1.0) + (4.0, 0.0)$) -- ($(-5.0, -1.0) + (4.0, 0.0)$) ($(-5.0, 1.0) + (6.0, 0.0)$) -- ($(-5.0, -1.0) + (6.0, 0.0)$) ($(-5.0, 1.0) + (8.0, 0.0)$) -- ($(-5.0, -1.0) + (8.0, 0.0)$);
\draw ($(8.0, 1.0) + (0.0, -6.0)$) rectangle ($(-8.0, -1.0) + (0.0, -6.0)$);
\draw ($(-8.0, 1.0) + (0.0, -6.0) + (2.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (2.0, 0.0)$) ($(-8.0, 1.0) + (0.0, -6.0) + (4.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (4.0, 0.0)$) ($(-8.0, 1.0) + (0.0, -6.0) + (6.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (6.0, 0.0)$) ($(-8.0, 1.0) + (0.0, -6.0) + (8.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (8.0, 0.0)$) ($(-8.0, 1.0) + (0.0, -6.0) + (10.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (10.0, 0.0)$) ($(-8.0, 1.0) + (0.0, -6.0) + (12.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (12.0, 0.0)$) ($(-8.0, 1.0) + (0.0, -6.0) + (14.0, 0.0)$) -- ($(-8.0, -1.0) + (0.0, -6.0) + (14.0, 0.0)$);
\node (x) at (0.0, 4.0) {\fontsize{28}{28}\selectfont $x$};
\draw[->] ($(x) + (0.0, -1.0)$) -- ($(-4.0, 1.25) + (0.0, 0.0)$);
\draw[->] ($(x) + (0.0, -1.0)$) -- ($(-4.0, 1.25) + (2.0, 0.0)$);
\draw[->] ($(x) + (0.0, -1.0)$) -- ($(-4.0, 1.25) + (4.0, 0.0)$);
\draw[->] ($(x) + (0.0, -1.0)$) -- ($(-4.0, 1.25) + (6.0, 0.0)$);
\draw[->] ($(x) + (0.0, -1.0)$) -- ($(-4.0, 1.25) + (8.0, 0.0)$);
\draw[->] ($(-4.0, -1.25) + (0.0, 0.0)$) to[in=80, out=200] ($(-7.0, 1.25) + (0.0, -6.0) + (0.0, 0.0)$) ;
\draw[->] ($(-4.0, -1.25) + (2.0, 0.0)$) to[in=140, out=-90] ($(-7.0, 1.25) + (0.0, -6.0) + (12.0, 0.0)$) ;
\draw[->] ($(-4.0, -1.25) + (4.0, 0.0)$) to[in=90, out=-90] ($(-7.0, 1.25) + (0.0, -6.0) + (10.0, 0.0)$);
\draw[->] ($(-4.0, -1.25) + (6.0, 0.0)$) to[in=80, out=-90] ($(-7.0, 1.25) + (0.0, -6.0) + (4.0, 0.0)$);
\draw[->] ($(-4.0, -1.25) + (8.0, 0.0)$) to[in=80, out=-30] ($(-7.0, 1.25) + (0.0, -6.0) + (14.0, 0.0)$);
\node at ($(-4.0, 0.0) + (0.0, 0.0)$) {\fontsize{20}{38}\selectfont $h_1$};
\node at ($(-4.0, 0.0) + (2.0, 0.0)$) {\fontsize{20}{38}\selectfont $h_2$};
\node at ($(-4.0, 0.0) + (4.0, 0.0)$) {\fontsize{20}{38}\selectfont $h_3$};
\node at ($(-4.0, 0.0) + (6.0, 0.0)$) {\fontsize{12}{38}\selectfont $\dots$};
\node at ($(-4.0, 0.0) + (8.0, 0.0)$) {\fontsize{20}{38}\selectfont $h_k$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (0.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_1$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (2.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_2$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (4.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_3$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (6.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_4$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (8.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_5$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (10.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_6$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (12.0, 0.0)$) {\fontsize{12}{38}\selectfont $\dots$};
\node at ($(-7.0, 0.0) + (0.0, -6.0) + (14.0, 0.0)$) {\fontsize{20}{38}\selectfont $b_m$};
\end{tikzpicture}
\end{tikzfigure*}](../images/latex/log-bloomfilters-debunked_89aa6891f76307d130d5de73a0466909b5691b67.png) 1
1
Thus, in the case that the bits are independent, the probability that
this will occur is simply 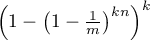 , thereby concluding the proof.
, thereby concluding the proof.
Makes sense? Seems correct? Well…
Crucially, this final step only works if the bits selected by the hash
function end up all being distinct, which is not always guaranteed
(even though the hash functions are assumed to be independent) - for
a simple counterexample, consider the case in which all the hash
functions happen to map the same bit - in this case the probability of
a false positive (given the hash outcomes) will be 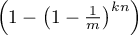 and not
and not 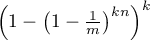 .
.
So clearly this is not the correct expression for the false positive of a bloom filter. So what is?
True false positive rate.
In fact, 30 years after Bloom's original publication3 (1970), this error was noticed by subsequent researchers Bose et al. in a 2008 paper (see here).
In order to correct this issue, Bose et al. propose an alternative derivation which uses a balls-into-bins analogy to account for the possibility that the hash outputs overlap, and derive the false positive rate as being (see here for the Coq proof):
![\[
\frac{1}{m^{k(n + 1)}} \sum_{i = 1}^{m} i^k i! {m \choose i} \stirlingsnd{kn}{i}
\]](../images/latex/log-bloomfilters-debunked_3940bf64a44304251c88c92c153aeb071386bd7a.png)
Unfortunately, while we now know that this new expression for the false positive rate is correct, 2 years after Bose et al.'s publication, other researchers actually found errors4 in their derivation, throwing further doubt on its validity.
This finally brings us to our research - Ceramist: Certifying Certainty and Uncertainty in Approximate Membership Query Structures, in which we manage to finally pin down the true behaviours of a Bloom filter by producing a certified proof of Bose et al.'s updated bound5 in Coq.
As we've proven this from first principles, it is highly unlikely any further errors will ever be discovered in this derivation, and as such we can be fairly certain that this new expression does actually model the behaviours of a Bloom filter correctly.
Interested? Learn more…
This concludes the high-level overview of the context surrounding our research and its importance6. Hopefully this has piqued your interest; there are many components of the work that I have not mentioned here for size constraints, such as:
- How can we encode probability in Coq?
- What is the exact derivation for the updated Bloom filter false positive expression?
- How can we extend this analysis to other probabilistic data
structures, such as:
- Counting filters?
- Quotient filters?
- Blocked Bloom filters?
(As a side product of the insight gained during our mechanisation, we even managed to construct a few entirely novel data structures - see the paper for more details).
If you are interested, I'd recommend either reading our full paper (see here), or checking out my presentation of the paper for CAV (see here).
The code and proofs used in this research project are FOSS, and can be found on the Ceramist repo: https://github.com/certichain/ceramist
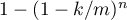 ,
which Bloom accurately derives.
,
which Bloom accurately derives.
 .
This claim is still wrong even though the hash outputs are guaranteed
to not overlap ( the "obvious" counterexample presented in the
article).
.
This claim is still wrong even though the hash outputs are guaranteed
to not overlap ( the "obvious" counterexample presented in the
article).
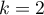 , and
, and  . First, observe that as
Bloom correctly derives, the probability of any single bit being
raised after an insertion is
. First, observe that as
Bloom correctly derives, the probability of any single bit being
raised after an insertion is  . Now, if after inserting 1
element, we learn that bit
. Now, if after inserting 1
element, we learn that bit 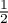 , either
, either 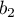 or
or 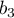 is raised (from the
from that hash outputs must be distinct). As such, the bits are not
independent:
is raised (from the
from that hash outputs must be distinct). As such, the bits are not
independent: ![$P[ b_2\text{ is raised} | b_1\text{ is raised} ] \neq P[ b_2\text{ is raised}]$](../images/latex/log-bloomfilters-debunked_f206256d70f4c45c07f513837a1924f60c4a21ae.png) (
(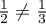 ).
).